Reinversion of control with continuations
In my last post I mentioned how it is possible to achieve a form of “reinversion of control” by using (green) threads. Some commenters noted how this is effectively a solved problem, as demonstrated for example by Erlang, as well as the numerous variations on CSP currently gaining a lot of popularity.
I don’t disagree with that, but it’s just not the point of this series of posts. This is about understanding the computational structure of event-driven code, and see how it’s possible to transform it into a less awkward form without introducing concurrency (or at least not in the traditional sense of the term).
Using threads to solve what is essentially a control flow problem is cheating. And you pay in terms of increased complexity, and code which is harder to reason about, since you introduced a whole lot of interleaving opportunities and possible race conditions. Using a non-preemptive concurrency abstraction with manual yield directives (like my Python gist does) will solve that, but then you’d have to think of how to schedule your coroutines, so that is also not a complete solution.
Programmable semicolons
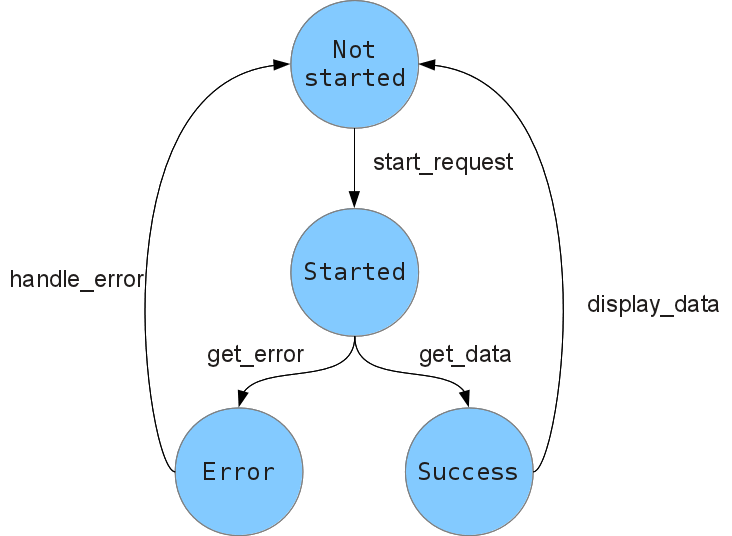
To find an alternative to the multitask-based approach, let’s focus on two particular lines of the last example:
reply = start_request(); get_data(reply)
where I added an explicit semicolon at the end of the first line. A semicolon is an important component of an imperative program, even though, syntactically, it is often omitted in languages like Python. It corresponds to the sequencing operator: execute the instruction on the left side, then pass the result to the right side and execute that.
If the instruction on the left side corresponds to an asynchronous operation, we want to alter the meaning of sequencing. Given a sequence of statements of the form
x = A(); B(x)
we want to interpret that as: call A, then return control back to the main loop; when A is finished, bind its result to x, then run B.
So what we want is to be able to override the sequencing operator: we want programmable semicolons.
The continuation monad
Since it is often really useful to look at the types of functions to understand how exactly they fit together, we’ll leave Python and start focusing on Haskell for our running example.
We can make a very important observation immediately by looking at the type of the callback registration function that our framework offers, and try to interpret it in the context of controlled side effects (i.e. the IO monad). For Qt, it could look something like:
connect :: Object -> String -> (a -> IO ()) -> IO ()
to be used, for example, like this:
connect httpReply "finished()" $ \_ -> do putStrLn "request finished"
so the first argument is the object, the second is the C++ signature of the signal, and the third is a callback that will be invoked by the framework whenever the specified signal is emitted. Now, we can get rid of all the noise of actually connecting to a signal, and define a type representing just the act of registering a callback.
newtype Event a = Event { on :: (a -> IO ()) -> IO () }
Doesn’t that look familiar? It is exactly the continuation monad transformer applied to the IO monad! The usual monad instance for ContT perfectly captures the semantics we are looking for:
instance Monad Event where return x = Event $ \k -> k x e >>= f = Event $ \k -> on e $ \x -> on (f x) k
The return function simply calls the callback immediately with the provided value, no actual connection is performed. The bind operator represents our custom semicolon: we connect to the first event, and when that fires, we take the value it yielded, apply it to f, and connect to the resulting event.
Now we can actually translate the Python code of the previous example to Haskell:
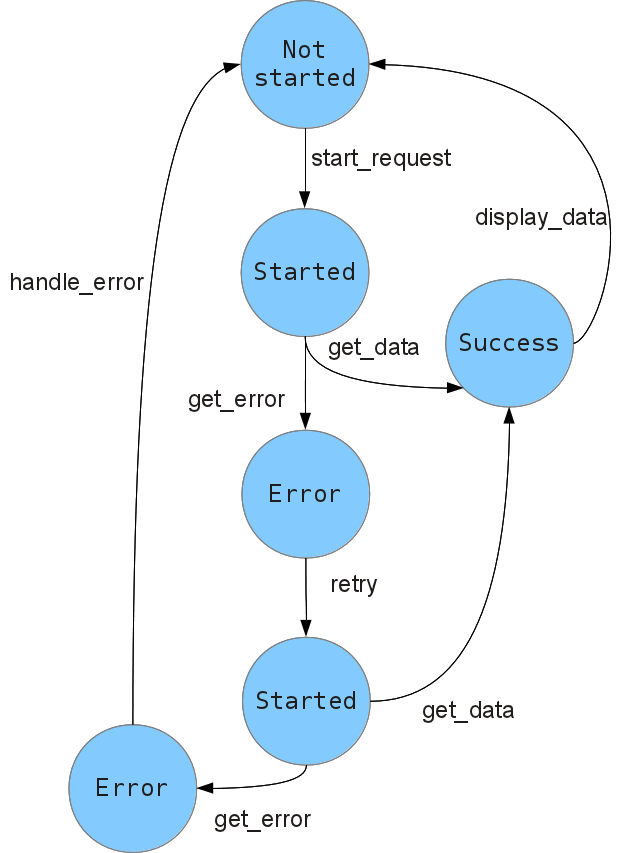
ex :: Event () ex = forever $ do result <- untilRight . replicate 2 $ do reply <- startRequest either (return . Left) (liftM Right . getData) reply either handleError displayData result untilRight :: Monad m => [m (Either a b)] -> m (Either a b) untilRight [m] = m untilRight (m : ms) = m >>= either (const (untilRight ms)) (return . Right)
Again, this could be cleaned up by adding some error reporting functionality into the monad stack.
Implementing the missing functions in terms of connect is straightforward. For example, startRequest will look something like this:
startRequest :: Event (Either String Reply) startRequest = Event $ \k -> do reply <- AccessManager.get "http://example.net" connect reply "finished()" $ \_ -> k (Right reply) connect reply "error(QString)" $ \e -> k (Left e)
where I took the liberty of glossing over some irrelevant API details.
How do we run such a monad? Well, the standard runContT does the job:
runEvent :: Event () -> IO () runEvent e = on $ \k -> return ()
so
runEvent ex
will run until the first connection, return control to the main loop, resume when an event occurs, and so on.
Conclusion
I love the simplicity and elegance of this approach, but unfortunately, it is far from a complete solution. So far we have only dealt with “one-shot” events, but what happens when an event fires multiple times? Also, as this is still very imperative in nature, can we do better? Is it possible to employ a more functional style, with emphasis on composability?
I’ll leave the (necessarily partial) answers to those questions for a future post.